Kriging, Inverse Distance Weighting (IDW) and other statistical algorithms are ways to perform interpolation on a set of data. Where these algorithms are useful is when you have some samples of an area but you want to get an impression of the whole area.
 Consider, for example, that there has been an oil spill in a certain area, and that engineers have taken samples of the area, measuring for hydrocarbons. They give the samples to you and ask you to provide a picture of the entire area.
Consider, for example, that there has been an oil spill in a certain area, and that engineers have taken samples of the area, measuring for hydrocarbons. They give the samples to you and ask you to provide a picture of the entire area.
You convert the samples to values of 1, 2, or 3, depending on how high the hydrocarbon level is in the sample and put the samples on a map. The samples clearly show the level of hydrocarbons in those sample area. But what about the rest of the area?

Here is where interpolation can be useful. You can use these algorithms to estimate values between the samples. Each algorithm provides a different estimate. For example, Kriging shows a gradual progression of values heading toward the lower right of the map.

On the other hand, IDW to Power 3 shows a concentration in the lower right of the map.
Which is right? Actually neither is guaranteed to be 100% accurate. Each has its characteristics, its strengths, its weakness. The important point is that interpolation techniques like kriging and Inverse Distance Weighting help us to visualize what areas might look like, given a set of samples of the area. In GIS, being close to accurate is often the best that you can do.

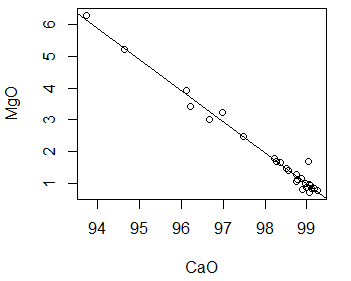
 It is a scatterplot where each point represents the value of magnesium for a given value of calcium in limestone.
It is a scatterplot where each point represents the value of magnesium for a given value of calcium in limestone.